[from the Royal Society of Chemistry’s Chemistry World, by Patrick de Jongh]
Results from a study combining experiments and simulations could overturn the assumption that amorphous forms of the same compound have the same molecular arrangement. The team behind the work claims to have prepared three amorphous forms of the diuretic drug hydrochlorothiazide and determined that they have distinct properties and distinct types of disorder. ‘If polyamorphism is proved in the future to be a universal—or at least not a very rare—phenomenon, then the pharmaceutical industry will need to make screens for polyamorphism and this will also be an opportunity for patenting,’ comments Inês Martins, from the University of Copenhagen in Denmark, who led the work with Thomas Rades.
Crystalline active pharmaceutical ingredients (APIs) often suffer from poor solubility. A common strategy to circumvent this problem is converting APIs into their amorphous form. This has been demonstrated for various APIs, including hydrochlorothiazide. However, the physical properties of polyamorphs are dependent on how they were prepared. Given there are no straightforward techniques to study how molecules interact and organise themselves in amorphous materials, the area is poorly understood.
Nevertheless, a team surrounding Rades and Martins set out to identify how amorphous forms of the same API, presenting different physicochemical properties, differ from each other. They decided to study hydrochlorothiazide as it was previously shown to have polyamorphs with glass transition temperatures above room temperature, which facilitates the preparation, isolation and analysis of its different polyamorphs. Starting from crystalline hydrochlorothiazide, they produced three polyamorphs: polyamorph I via spray-drying, polyamorph II via quench-cooling and polyamorph III by ball-milling. Thermal analysis revealed a significantly lower glass-transition temperature for polyamorph I (88.7°C), whereas polyamorphs II and III had similar glass-transition temperatures (117.5°C and 119.7°C, respectively). The polyamorphs also demonstrated very different shelf-life stabilities against crystallisation.
Subsequently, they studied polyamorphic interconversions by submitting the polyamorphs to the preparation conditions used for other polyamorphs. For example, polyamorph I (obtained by spray-drying) was subjected to quench–cooling or ball-milling. Identifying temperature as a critical parameter, they observed that polyamorph II could be obtained from polyamorphs I and III, but the reverse pathway was not possible. Meanwhile, they observed polyamorph I and polyamorph III interconvert. These results demonstrate polyamorph II is the most stable amorphous form.
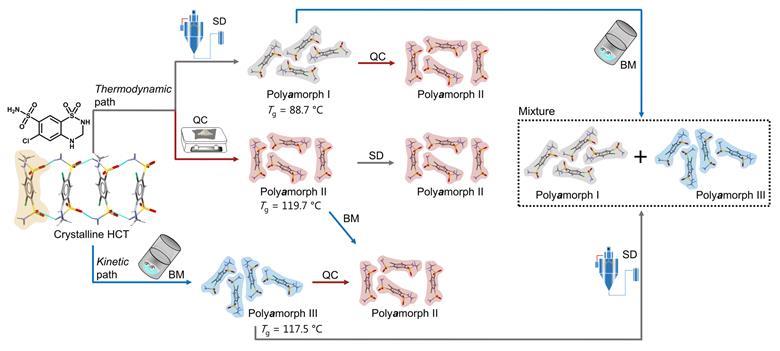
Researchers used a variety of techniques to elucidate the different polyamorphs that can be produced from crystalline hydrochlorothiazide and the polyamorphic interconversions that occur when a specific amorphous form is submitted to temperature or milling treatments
‘The problem out of the gate with polyamorphism as a concept is how to tell the difference between a well-defined metastable amorphous structure and an unrelaxed one that simply results from kinetically trapped defects introduced during processing. This is hard to define since the amorphous structure is statistical in any case,’ comments Simon Billinge, who studies the structure of disordered materials at Columbia University in the US. ‘They process the samples very differently. We know—from our own work—that this results in amorphous phases with very different stabilities against recrystallisation, for example, but is this polyamorphism? On the other hand, they find that the pair distribution functions of each of their “forms” are identical. There is no experimental evidence for a distinct structure. Taken together, the results do little to advance my understanding of polyamorphism.’
Distinct dihedral angle distributions
To get further information on how the polyamorphs are different on a molecular level, Martins and Rades turned to molecular dynamics simulations, comparing the dihedral angles around the sulfonamide groups in polyamorphs I and II. ‘Polyamorph I, which has a large number of the molecules with a dihedral angle similar to the one reported for crystalline hydrochlorothiazide, has a lower physical stability and faster structural relaxation time than polyamorph II, which has a broader dihedral angle distribution. Our findings indicate that a broader dihedral angle distribution seems to contribute to a better physical stability and slower structural relaxation,’ says Martins. They therefore hypothesise that having half the molecules with a conformation closer to crystalline hydrochlorothiazide and half of the molecules with a different conformation could help in establishing specific molecular arrangements that would favour the stability of the amorphous form.
The team also says the simulations corroborated its experimental results that polyamorph I can transform into polyamorph II, while the opposite conversion did not take place.
However, Billinge does not believe the computational studies provide conclusive evidence: ‘There is a detailed molecular dynamics analysis where different annealing conditions in the simulations give some slightly different statistics on the molecular conformations, but despite their claim, the resulting computed pair distribution functions do not look like the measured ones, so we have no way of knowing if the molecular dynamics is capturing what is happening in the real material. For amorphous materials, it is very difficult to equilibrate them in a molecular dynamics simulation, so you will be looking at artefacts of how the ensemble was created. Any claims to have found polyamorphism from molecular dynamics simulations by themselves are therefore questionable.’
Rades says their results can change the field of pharmaceutics: ‘We expect that other drug molecules may exhibit polyamorphism and the question would be which structural parameters would be different. In the case of hydrochlorothiazide, the dihedral angle distribution was found to be a parameter contributing for the formation of different polyamorphs. In other drugs, maybe the dihedral angle distribution (molecular conformations) could be different as well, but also maybe the type of intermolecular interactions can play a more important role in the formation of polyamorphs.’
The team now hope the pharmaceutical industry will look at amorphous systems differently and not assume that all amorphous forms of the same compound are the same. ‘Knowing this and considering that a certain polyamorph will have better physical stability, solubility or dissolution properties than another polyamorph, this will be an opportunity for the pharmaceutical industry to prepare tablets of a drug where the dose could be lower than tablets containing the crystalline form,’ concludes Rades.